カテゴリ
月別 アーカイブ
- 2025年4月 (6)
- 2025年3月 (27)
- 2025年2月 (24)
- 2025年1月 (27)
- 2024年12月 (28)
- 2024年11月 (18)
- 2024年10月 (22)
- 2024年9月 (24)
- 2024年8月 (20)
- 2024年7月 (20)
- 2024年6月 (21)
- 2024年5月 (22)
- 2024年4月 (37)
- 2024年3月 (26)
- 2024年2月 (18)
- 2024年1月 (22)
- 2023年12月 (23)
- 2023年11月 (17)
- 2023年10月 (18)
- 2023年9月 (20)
- 2023年8月 (12)
- 2023年7月 (20)
- 2023年6月 (28)
- 2023年5月 (25)
- 2023年4月 (30)
- 2023年3月 (22)
- 2023年2月 (20)
- 2023年1月 (28)
- 2022年12月 (24)
- 2022年11月 (26)
- 2022年10月 (28)
- 2022年9月 (24)
- 2022年8月 (21)
- 2022年7月 (15)
- 2022年6月 (18)
- 2022年5月 (15)
- 2022年4月 (20)
- 2022年3月 (21)
- 2022年2月 (22)
- 2022年1月 (17)
- 2021年12月 (20)
- 2021年11月 (20)
- 2021年10月 (21)
- 2021年9月 (20)
- 2021年8月 (22)
- 2021年7月 (20)
- 2021年6月 (22)
- 2021年5月 (26)
- 2021年4月 (26)
- 2021年3月 (16)
- 2021年2月 (17)
- 2021年1月 (22)
- 2020年12月 (18)
- 2020年11月 (20)
- 2020年10月 (20)
- 2020年9月 (22)
- 2020年8月 (22)
- 2020年7月 (23)
- 2020年6月 (19)
- 2020年5月 (26)
- 2020年4月 (28)
- 2020年3月 (26)
- 2020年2月 (21)
- 2020年1月 (31)
- 2019年12月 (31)
- 2019年11月 (20)
- 2019年10月 (24)
- 2019年9月 (17)
- 2019年8月 (2)
- 2019年7月 (1)
- 2019年6月 (1)
- 2018年9月 (1)
- 2018年7月 (2)
- 2018年6月 (1)
- 2018年3月 (1)
- 2017年6月 (1)
- 2016年9月 (1)
HOME > スク玉ブログ > 算数は積み重ねの科目~一瞬で解き方がわかれば天才だ~
スク玉ブログ
算数は積み重ねの科目~一瞬で解き方がわかれば天才だ~
小学校の算数が一番難しいと思う さんなん です。文字は使えないし、円周率も3.14で計算しないといけませんからね。そして、何よりパズル的要素が大きいのも理由の1つですね。
さて、「突然ですが問題です!」シリーズをお届けします。
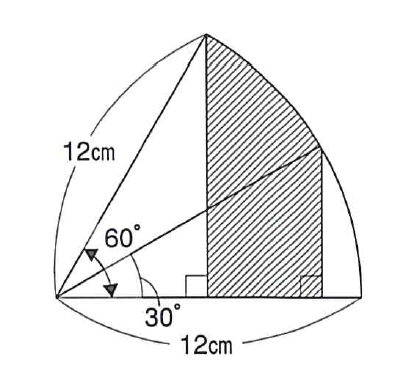
問)斜線の部分の面積を求めなさい。
パッと見ると難しいのですが、意外とすぐ解けます。
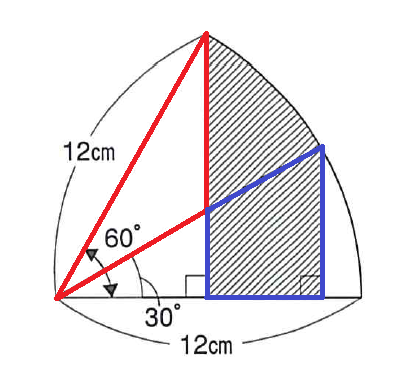
簡単に説明すると、下図の赤い部分と青い部分の面積が同じになります。
なぜ面積が同じになるのか、「三角形の合同」がヒントです(どことどこの三角形かは考えてください。ちなみに「合同」は小学生で習いますよ。)
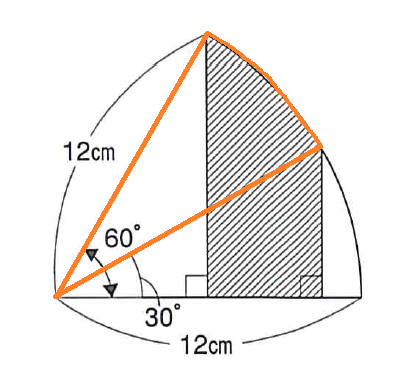
つまり、下図のオレンジ色の面積を求めればよいのです。
よって答えは、
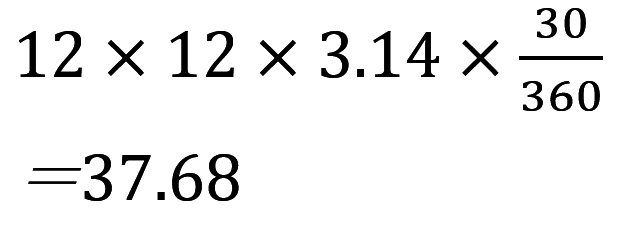
となります。いかがでしょうか。
そして、もう1問。おかわり。
安心してください。きっとブログを読んでるお母さん方は、もうお腹いっぱいだと思うので解きませんから。
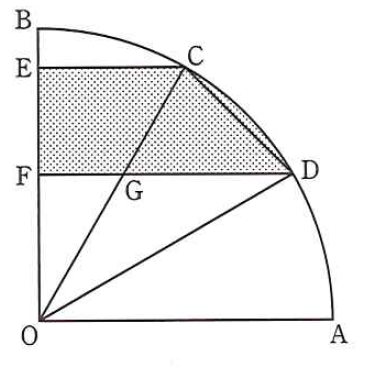
問)斜線の部分の面積は、おうぎ形OABの面積の何倍か?
そもそも「長さがないと解けねーじゃん」とも聞こえてきそうですが、解きませんので実際の問題文は割愛します。
ここで言いたいことは、この問題の解き方は先ほど説明した問題と同じだってこと。
つまり斜線の部分の面積は、おうぎ形ODCの面積と等しくなるのです。解き方を知っていれば、一瞬で解けちゃいます。
ちなみにこの問題は、過去の愛知県の公立高校入試で出題されたもの。
今なら解けそうじゃないですか。解けそうだから、解きたくなりませんか(笑)。
数学って、1度目に解けなくてもいいんです。間違い直しに時間をかけて、ちゃんと説明できるまで理解して、自分の中での着々と解法を増やしていく。
テストや入試までに、この準備しておくのです。だから問題演習って大事なんです。ただ、自分で噛み砕かないと定着しませんのでご注意ください。
ちょうど中1生は、おうぎ形の単元も学年末テストの範囲だと思うので、知らなければこの解き方はぜひ覚えておきましょうね。
本当は小学生の内からこんな問題をたくさん演習して欲しいけど、基礎学力の格差で教育現場はそれどころじゃない。
だからスク玉では、教科書内容の学習が終わった生徒から総復習として、こういった問題に取り組んでもらっています。
コツコツ積み重ねていく。
もし勉強のスタートが遅かった場合は、今たくさん解いて前を走っている子に喰らいついていきましょう。
《小学部》新小4~新小6
2024年3月18日(月)~新学年の勉強を始めます!

《中学部》
新中2・新中3は2024年3月1日~新学年の勉強開始します!
新中1は3月18日(月)から中1の勉強を始めます!

《高校部》
新高3はこの冬から受験勉強をはじめています!
新高2はこの冬で英文法完成→精読!数学は12月~数ⅠAの総復習開始!
新高1は公立高校入試後に、高1の勉強開始!

受験準備コース 高1春~(週2日~数学・英語優先)
受験対策コース 高2冬~(週2日、個別指導含む)

(LINE@登録でお問合せ【お問合せ専用】)

ー・-・-・-・-・-・-・-・-・-・-・-・-・-
スク玉ブログ連絡用LINE@を作りました。よかったらご登録ください。(塾生の方も、塾生でない方もどうぞ)
※塾連絡は、塾生専用のLINE@にてご連絡します。
↓↓↓このLINE@の用途は、スク玉ブログの更新のみ↓↓↓

さて、「突然ですが問題です!」シリーズをお届けします。

問)斜線の部分の面積を求めなさい。
パッと見ると難しいのですが、意外とすぐ解けます。
簡単に説明すると、下図の赤い部分と青い部分の面積が同じになります。
なぜ面積が同じになるのか、「三角形の合同」がヒントです(どことどこの三角形かは考えてください。ちなみに「合同」は小学生で習いますよ。)

つまり、下図のオレンジ色の面積を求めればよいのです。

よって答えは、
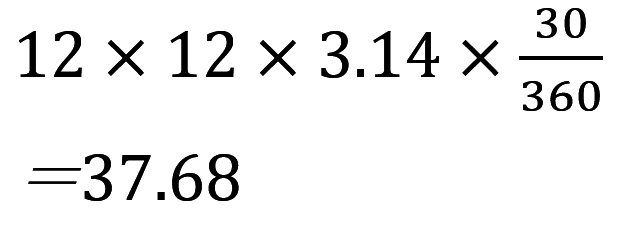
となります。いかがでしょうか。
そして、もう1問。おかわり。
安心してください。きっとブログを読んでるお母さん方は、もうお腹いっぱいだと思うので解きませんから。

問)斜線の部分の面積は、おうぎ形OABの面積の何倍か?
そもそも「長さがないと解けねーじゃん」とも聞こえてきそうですが、解きませんので実際の問題文は割愛します。
ここで言いたいことは、この問題の解き方は先ほど説明した問題と同じだってこと。
つまり斜線の部分の面積は、おうぎ形ODCの面積と等しくなるのです。解き方を知っていれば、一瞬で解けちゃいます。
ちなみにこの問題は、過去の愛知県の公立高校入試で出題されたもの。
今なら解けそうじゃないですか。解けそうだから、解きたくなりませんか(笑)。
数学って、1度目に解けなくてもいいんです。間違い直しに時間をかけて、ちゃんと説明できるまで理解して、自分の中での着々と解法を増やしていく。
テストや入試までに、この準備しておくのです。だから問題演習って大事なんです。ただ、自分で噛み砕かないと定着しませんのでご注意ください。
ちょうど中1生は、おうぎ形の単元も学年末テストの範囲だと思うので、知らなければこの解き方はぜひ覚えておきましょうね。
本当は小学生の内からこんな問題をたくさん演習して欲しいけど、基礎学力の格差で教育現場はそれどころじゃない。
だからスク玉では、教科書内容の学習が終わった生徒から総復習として、こういった問題に取り組んでもらっています。
コツコツ積み重ねていく。
もし勉強のスタートが遅かった場合は、今たくさん解いて前を走っている子に喰らいついていきましょう。
《小学部》新小4~新小6
2024年3月18日(月)~新学年の勉強を始めます!

《中学部》
新中2・新中3は2024年3月1日~新学年の勉強開始します!
新中1は3月18日(月)から中1の勉強を始めます!


《高校部》
新高3はこの冬から受験勉強をはじめています!
新高2はこの冬で英文法完成→精読!数学は12月~数ⅠAの総復習開始!
新高1は公立高校入試後に、高1の勉強開始!

受験準備コース 高1春~(週2日~数学・英語優先)
受験対策コース 高2冬~(週2日、個別指導含む)

(LINE@登録でお問合せ【お問合せ専用】)

ー・-・-・-・-・-・-・-・-・-・-・-・-・-
スク玉ブログ連絡用LINE@を作りました。よかったらご登録ください。(塾生の方も、塾生でない方もどうぞ)
※塾連絡は、塾生専用のLINE@にてご連絡します。
↓↓↓このLINE@の用途は、スク玉ブログの更新のみ↓↓↓

2024年2月 1日 10:42





